Potential Energy Of A Dipole In An External Electric Field

#6. Potential Energy Of A Dipole In An External Electric Field

Consider a dipole placed in a uniform electric field at an angle ‘θ’ with the electric field. The torque experience by the dipole is 

Torque ( τ ) = Force x perpendicular distance

Here the perpendicular distance is BC. From the triangle ABC we can find the distance BC

sin⁡θ =  BC/2l i.e, BC= 2l sin θ 

by applying value of BC we get 

Torque ( τ ) =  Force x 2l sin θ 

                    = q E 2l sin θ

                    = P E sin θ      [q(2l)= dipole moment P]

                    = P x E  

Now , Torque ( τ ) = P E sin θ 

Work done to move a dipole in an external electric field will stored as potential energy, So to  find the work done we have to move the dipole at an angle of dθ

d w = τ x dθ

       = P E sinθ dθ

w = ∫P E sinθ dθ

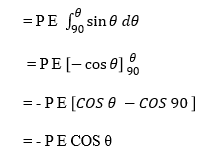
w = U (P.E) = - P . E

  

Browse more topics under Electrostatic Potential & Capacitance

• Electrostatic Potential, Potential Energy, Potential Energy Difference
• Potential Due To A Point Charge
• Potential Due To An Electric Dipole
• Equipotential Surface & Its Properties
• Potential Energy In An External Electric Field
• Potential Energy Due To A Single Charge In An External Electric Field
• Potential Energy Due To A System Of 2 Charges In An External Electric Field
• Potential Energy Due To An Electric Dipole In An External Electric Field
• Electrostatics Of The Conductor
• Dielectric And Polarization
• Capacitor And Capacitance
• Parallel Plate Capacitor
• Effect Of Dielectric On A Capacitor
• Energy Stored In A Capacitor
• Van De Graaff Generator